总结优化算法收敛性证明的两类方法

这篇文章中，我们总结两类做数值优化迭代算法收敛性证明的方法，同时也讨论了优化算法设计的思路。

数值优化在工程应用中有非常重要的作用。但在使用优化算法时候，算法的收敛性是我们需要认真考虑的东西，例如我们需要知道梯度下降是一阶收敛而牛顿法是二阶收敛，因此一般情况下，牛顿法会比梯度下降运行更快。了解收敛性后，我们才能更好地应用算法。这里，我们总结两类做数值算法收敛性证明的方法，同时讨论以后我们自己设计算法的思路。

该类中，收敛性的证明多使用不动点定理(Fixed Point Theorems)进行证明。不动点定理(Fixed Point Theorems)是数学证明中一个非常重要的定理，许多重要的数学定理都是由不动点定理证明的，例如偏微分方程解的存在性、博弈论中纳什均衡点的存在性以及我们这里即将介绍的数值算法的收敛性等。我们首先介绍一下不动点定理，然后介绍如何使用不动点定理进行算法收敛性证明。

简单地说，对一个函数, 如果有一个点，使得，那么我们称为的一个不动点。例如对于函数，任意一点都是的不动点，对于，为的不动点。但并不是所有的函数都是有不动点的，例如就不具有不动点。那么一个自然的问题就是在具有什么样的条件下有不动点呢？这里我们介绍巴拿赫固定点定理(Banach Fixed Point Theorem)。

巴拿赫固定点定理：对于函数，其中为以为源点，为半径的球，如果存在一个数, 使得
那么，具有唯一一个不动点，即,并且我们能通过下列方法来找到：找一个初始点，并按照的方法生成一个序列，那么我们有收敛到。我们称为压缩映射(contraction mapping)。

注意到巴拿赫固定点定理不仅给出了不动点的存在性，而且给出了唯一性以及构造不动点的办法。那么我们如何使用这个不动点定理来进行算法收敛性证明和指导算法设计呢？给定一个算法，为了证明其收敛性，我们可以将算法的每一次迭代看做一个函数，算法第次的输入为而输出为，那么我们首先需要证明为压缩映射，即满足性质，根据巴拿赫固定点定理，我们就有的固定点存在，即我们的整个算法收敛。反过来，如果我们要设计一个迭代算法，求解一个值，那么我们需要构造一个压缩映射，将作为的一个不动点，再以任意一个初值出发，按照的迭代方式，生成序列，最终当迭代次数足够多的时候，将离非常接近，即为的一个好的估计值。

下面我们通过例子来介绍巴拿赫固定点定理如何指导算法的设计，详细的证明可以参见更专业的书籍或者论文。

这里我们考虑下列问题

这里我们假设足够的光滑，具有很好的性质。那么根据微积分里的定理，如果为上述问题的解，那么满足

其中为的梯度。 如果我们想使用巴拿赫不动点定理来设计一个算法求解，那么，我们必须找到一个函数，将作为的不动点，并且在不动点处，能满足条件。如何寻找这么一个函数呢？我们可以从最简单的开始，将取负后两边同时加上一个，我们得到

我们定义，那么即为的一个不动点，所以我们可能会期望按照算法的方式生成一个序列并且会收敛到。这时，我们需要使用巴拿赫固定点定理。我们得去验证是否是一个压缩映射，即是否满足条件，我们会做下列的计算。假设为中的一点，我们有

观察上述式子，我们知道对于一般的函数，上述式子并不会给出的结果。因此，我们需要限定的讨论范围。我们假设满足下列性质：存在, ，使得

那么，根据，我们有

因此，要使得满足条件，我们需要，即。那么我们可以有下列定理

假设足够光滑且满足和，并且，定义函数，那么有唯一一个不动点，且满足。从开始，我们按照下列方式生成一个序列，
则收敛到。

可以观察到，如果我们取，在的不动点处，我们仍然有，看起来如此定义的也是一个生成迭代算法的好的函数。但是是否满足压缩映射的假设呢？读者可以试着进行的计算来查看会发生什么事情。并且思考如何改变与的假设使得计算能够进行下去，思考你改的假设是否合理等等问题。

对算法熟悉的读者知道，由生成的迭代算法即为梯度下降算法。类似的构造算法还有牛顿法，我们可以取

其中为的二阶导数。因此，如果在的不动点处，可逆，我们有，即

上述式子给出，即为的一个极值点。读者可以搜索相关文献查阅为压缩映射需要满足的条件。

这里我们考虑下列优化问题

问题在图像处理、最优传输，最优控制等问题中都有出现。我们可以将看做一个函数，再使用梯度下降来求解。然而由于是两个函数的和，我们又可以采用这个特点设计新的算法。为了更清楚的说明整个思想，我们假设和都是足够光滑的，即我们可以求和的导数。虽然以下算法的威力在和其中一个不可求导的时候才能体现出来，但这样可以让我们在这里避免讨论像子导数(Subgradient)的概念，专注算法的设计思想。

根据微积分的定理，我们知道如果为中的最小值点，那么我们有

类似上一节中我们构造梯度下降的生成函数的思路，我们需要根据的条件，将表示为某个函数的不动点。下面我们介绍几种算子的划分算法。

• Forward-Backward Splitting. 从，我们可以得到

将的两边同时加上，我们得到

其中为Identity Map，即对任意的，我们有。在中，我们将算子求逆，得到

因此，我们可以定义

即为的一个不动点。我们可以使用生成算法

可以看出为沿着的负梯度方向进行一次梯度下降，而为沿着的梯度方向找到梯度上升后能够到达的位置的点。因此，被称作Forward-Backward Splitting。读者可以查看相关文献查阅为压缩算子所需要的的条件。

• Douglas-Rachford Splitting 这里，为了书写的方便，我们定义

并定义

其中为区间的一个实数。读者可以验证如果是的不动点，那么根据得到的满足，因此，我们可以使用函数来生成迭代算法。读者可以参考论文Linear Convergence and Metric Selection for Douglas-Rachford Splitting and ADMM查阅为压缩映射所需要的条件。

注: 可以从上面例子看出，我们有非常多的方法来将优化算法的解表示为某个函数的不动点，然后根据函数来生成算法。但是并不是每一个这样构造的算法都收敛。为了保证收敛性，我们需要构造的函数是压缩映射。

这里我们仍然考虑单个函数的优化，我们试图解决下列优化问题

假设为函数的最小值点。我们采用某种迭代算法来计算，记为第步迭代计算所得的值。为了证明该算法的收敛性，我们找到一个能量函数，（一般叫做Lyapunov函数），该函数度量了与之间的某种距离。我们将该能量函数记做，能量函数必须是大于等于零的。然后我们证明为递减的函数，即对任意的，我们有

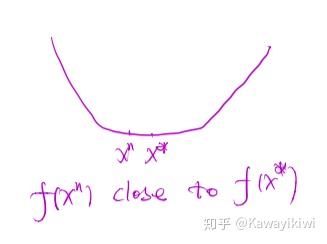
直觉上讲，描述的是在迭代过程中，随着迭代次数增加，离越来越近，我们的算法在收敛。

下面是几种常见的能量函数:

• 。 该函数度量了到的欧几里得距离，如果减小到足够小，那么可作为最小值点的近似值。读者可以参考Newton's Method中对牛顿法的收敛性证明。
  
• 。该函数度量的是函数值之间的距离，如果很小，那么离很近，但是可能离可能并不近，例如函数的底部非常的平坦，如下图所示，那么算法可能在离很远的地方就停下来了。因此使用该距离可能会产生较大的误差，需要根据函数的特性来定。对于此距离函数证明收敛性，可以参见 Gradient Descent and Acceleration对Nesterov加速算法的证明。

• ，其中为一个凸函数。函数定义了与之间的Bregman距离。可以参见A Variational Perspective on Accelerated Methods in Optimization。
  

当然，这里列出的能量函数并不完整，例如Fast alteranting direction optimization methods这篇文章中，使用原问题与对偶问题的优化条件的残差(Primal dual residuals)来定义能量函数。在实际问题中，对于具体的问题如何设计好能量函数，仍然是比较靠科研人员的直觉和经验。

这篇文章中，我们介绍了两类证明算法收敛性的方法：固定点类与能量函数类。对于固定点类的算法，我们讨论了如何基于固定点的思想来设计新的算法。这里的总结一定是不完全的，随着更多地阅读论文，以后有机会将更多的方法纳入这个归纳中。